2007-10-01
Abstract
Ángela Blanco and Manuel Martín-Merino describe how anti-spam filters can be boosted by using an ensemble of SVM classifiers.
Copyright © 2007 Virus Bulletin
Unsolicited Commercial Email (UCE) is becoming a nightmare for users of the Internet. Several machine-learning techniques have been applied to attempt to reduce the volume of spam that reaches end-users. Support Vector Machines (SVM) have achieved a high level of accuracy in filtering spam messages. However, one problem with classical SVM algorithms is that a high number of legitimate messages are misclassified as spam (false positive errors). These kinds of error are expensive and should be reduced as much as possible.
In this paper, we address the problem of reducing the number of false positive errors in anti-spam email filters without significantly increasing the number of false negative errors. To this end, an ensemble of SVMs that combines multiple dissimilarities is proposed. The experimental results suggest that our combination strategy outperforms classifiers that are based solely on a single dissimilarity as well as combination strategies such as bagging.
Unsolicited Commercial Email, also known as spam, has become a serious problem for Internet users and providers alike [10]. Several researchers have applied machine-learning techniques in order to improve the detection of spam messages. Naïve Bayes models are the most popular [2], but other authors have applied Support Vector Machines (SVM) [9], boosting and decision trees [6] with remarkable results. SVM is particularly attractive in this application because it is robust against noise and able to handle a large number of features [22].
Errors in anti-spam email filtering are strongly asymmetric. Thus false positive errors (or valid messages that are blocked), are prohibitively expensive. Several authors have proposed new versions of the original SVM algorithm that help to reduce the false positive errors [21], [15]. In particular, it has been suggested that combining non-optimal classifiers can help to reduce the variance of the predictor [21], [5], [3] and consequently reduce the misclassification errors. In order to achieve this goal, different versions of the classifier are usually built by sampling the patterns or the features [5]. However, in our application it is expected that the aggregation of strong classifiers will help to reduce the false positive errors further [19], [12], [8].
In this paper, we address the problem of reducing false positive errors by combining classifiers based on multiple dissimilarities. To achieve this, a diversity of classifiers is built considering dissimilarities that reflect different features of the data. The dissimilarities are first embedded into a Euclidean space where an SVM is adjusted for each measure. Next, the classifiers are aggregated using a voting strategy [14]. The method proposed has been applied to the Spam UCI machine-learning database [20] with remarkable results.
This article is organized as follows. In section 2 we will introduce the Support Vector Machines. Section 3 presents our method of combining SVM classifiers based on dissimilarities. Section 4 illustrates the performance of the algorithm in the challenging problem of spam filtering. Finally, in section 5 we present our conclusions.
SVM is a powerful machine-learning technique that is able to work efficiently with high-dimensional and noisy data. It has been proposed under a strong theoretical foundation using the Statistical Learning Theory [22].
Let {(xi, yi)}ni=1 be the training set codified in ℝd. We assume that each xi belongs to one of the two classes (spam, or not spam) labelled by yi ∈ {-1, +1}. The SVM algorithm looks for the linear hyperplane f (x; w) = wT x+b that minimizes the prediction error for new variants of spam that are not considered in the training set. Minimizing the prediction error is equivalent in the Statistical Learning Theory to maximizing the margin γ. Considering that γ = 2/||w||2, this is equivalent to minimizing the L2 norm of w. The slack variables ξi allow us to consider classification errors.
Figure 1 illustrates the linear hyperplane generated by the SVM and the meaning of the margin and the slack variables.
The hyperplane that minimizes the prediction error is given by the optimization problem shown in equation (1).
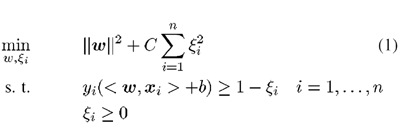
The first term in equation (1) determines the generalization ability of the SVM and the second term determines the error for the training set. C is a regularization parameter that determines the balance between the training error and the complexity of the classifier.
The SVM technique exhibits several interesting features for email anti-spam filtering. First, the optimization problem is quadratic and can be solved efficiently in the dual space [22]. Second, it can easily be extended to the non-linear case substituting the scalar products by a Mercer kernel [22]. Finally, SVM has a high generalization ability.
An important step in the design of a classifier is the selection of the proper dissimilarity that reflects the proximities among the objects. However, most classifiers such as the classical SVM algorithm are based implicitly on the Euclidean distance. The Euclidean dissimilarity is not suitable to reflect the proximities among the emails [16], [10]. The SVM algorithm has been extended to incorporate non-Euclidean dissimilarities [18]. However, different measures reflect different features of the dataset and no dissimilarity outperforms the others because each one misclassifies a different set of patterns.
In this section, we present an ensemble of classifiers based on multiple dissimilarities. The aim is to reduce the false positive errors of classifiers that are based on a single dissimilarity.
The original SVM algorithm is not able to work directly from a dissimilarity matrix. To overcome this problem, we follow the approach of [18]. First, the dissimilarities are embedded into a Euclidean space such that the inter-pattern distances reflect approximately the original dissimilarity matrix. This can be done through a Singular Value Decomposition (SVD). Next, the test points are embedded via a linear algebra operation. The mathematical details are provided in [4].
Next, we introduce our combination strategy for classifiers based on dissimilarities. Our method is based on the evidence that different dissimilarities reflect different features of the dataset. Therefore, classifiers based on different measures will misclassify a different set of patterns. Hence, we have considered eight complementary measures that reflect different features of the data (see [4]).
Figure 1 illustrates how the combination strategy reduces the number of misclassification errors. The bold patterns are assigned to the wrong class by only one classifier, but using a voting strategy the patterns will be assigned to the correct class.
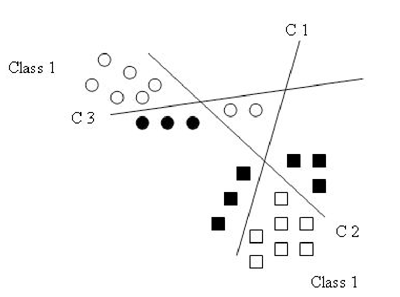
Figure 2. Aggregation of classifier using a voting strategy. Bold patterns are misclassified by a single hyperplane but not by the combination.
Our combination algorithm proceeds as follows: first, the dissimilarities introduced in this section are computed. Each dissimilarity is embedded into a Euclidean space. To increase the diversity among classifiers, once the dissimilarities are embedded several bootstrap samples are drawn. Next, we train an SVM for each dissimilarity and bootstrap sample. Thus, it is expected that misclassification errors will change from one classifier to another. So the combination of classifiers by a voting strategy will help to reduce the number of misclassification errors.
A related technique for combining classifiers is the bagging technique [5], [3]. This method generates a diversity of classifiers that are trained using several bootstrap samples. Next, the classifiers are aggregated using a voting strategy. Nevertheless, there are three important differences between bagging and the method proposed in this section.
First, our method generates the diversity of classifiers by considering different dissimilarities and thus will induce a stronger diversity among classifiers. A second advantage of our method is that it is able to work directly with a dissimilarity matrix. Finally, the combination of several dissimilarities avoids the problem of choosing a particular dissimilarity for the application we are dealing with – which is a difficult and time-consuming task.
The algorithm proposed can easily be applied to other classifiers based on dissimilarities such as the nearest neighbour algorithm.
In this section, the ensemble of classifiers proposed is applied to the identification of spam messages.
The spam collection considered is available from the UCI machine-learning database [20]. The corpus is made up of 4,601 emails, of which 39.4% are spam and 60.6% are legitimate messages. The number of features used to codify the emails is 57 and they are described in [20].
The dissimilarities have been computed without normalizing the variables because this preprocessing may increase the correlation among them. As we mentioned in section 3, the disparity among the dissimilarities will help to improve the performance of the ensemble of classifiers. Once the dissimilarities have been embedded in a Euclidean space, the variables are normalized to unit variance and zero mean. This preprocessing improves the SVM accuracy and the speed of convergence.
Regarding the ensemble of classifiers, an important issue is the dimensionality in which the dissimilarity matrix is embedded. To this end, a metric Multidimensional Scaling Algorithm is run. The number of eigenvectors considered is determined by the curve induced by the eigenvalues. For the problem at hand, the first 20 eigenvalues preserve the main structure of the dataset.
The combination strategy proposed in this paper has also been applied to the k-nearest neighbour classifier. An important parameter in this algorithm is the number of neighbours which has been estimated using 20% of the patterns as a validation set.
The classifiers have been evaluated from two different points of view: on the one hand we have computed the misclassification errors. But in our application, false positive errors are very expensive and should be avoided. Therefore, false positive errors are a good index of the algorithm performance and are also provided.
Finally, the errors have been evaluated considering a subset of 20% of the patterns drawn randomly without replacement from the original dataset.
Table 1 shows the experimental results for the ensemble of classifiers using the SVM. The method proposed has been compared with the bagging technique introduced in section 3 and with classifiers based on a single dissimilarity. The m parameter determines the number of bootstrap samples considered for the combination strategies. C is the standard regulation parameter in the C-SVM [22].
| Linear kernel | Polynomial kernel | |||
| Method | Error | False positive | Error | False positive |
| Euclidean | 8.1% | 4% | 15% | 11% |
| Cosine | 19.1% | 15.3% | 30.4% | 8% |
| Correlation | 18.7% | 9.8% | 31% | 7.8% |
| Manhattan | 12.6% | 6.3% | 19.2% | 7.1% |
| Kendall-τ | 6.5% | 3.1% | 11.1% | 5.4% |
| Spearman | 6.6% | 3.1% | 11.1% | 5.4% |
| Bagging | 7.3% | 3% | 14.3% | 4% |
| Combination | 6.1% | 3% | 11.1% | 1.8% |
Table 1. Experimental results for the ensemble of SVM classifiers. Classifiers based solely on a single dissimilarity and bagging with the Euclidean distance have been taken as reference. (Parameters: Linear kernel: C=0.1, m=20; Polynomial kernel: Degree=2, C=5, m=20)
Looking at Table 1, the following conclusions can be drawn:
The combination strategy improves significantly the Euclidean distance which is usually considered by most SVM algorithms.
The combination strategy with polynomial kernel reduces significantly the number of false positive errors generated by the best single classifier. The improvement is smaller for the linear kernel. This can be explained because the nonlinear kernel allows us to build classifiers with larger variance and therefore the combination strategy can achieve a larger improvement in the number of false positive errors.
The combination strategy outperforms a widely used aggregation method such as bagging. The improvement is particularly important for the polynomial kernel.
Table 2 shows the experimental results for the ensemble of k-NNs classifiers. k denotes the number of nearest neighbours considered. As in the previous case, the combination strategy proposed improves the false positive errors of classifiers based on a single distance. We also report that bagging is not able to reduce the false positive errors of the Euclidean distance. Besides, our combination strategy improves significantly the bagging algorithm. Finally, we observe that the misclassification errors are larger for k-NN than for the SVM algorithm. This can be explained because the SVM algorithm has a higher generalization ability when the number of features is large.
| Method | Error | False positive |
|---|---|---|
| Euclidean | 22.5% | 9.3% |
| Cosine | 23.3% | 14.0% |
| Correlation | 23.2% | 14.0% |
| Manhattan | 23.2% | 12.2% |
| Kendall-τ | 21.7% | 6% |
| Spearman | 11.2% | 6.5% |
| Bagging | 19.1% | 11.6% |
| Combination | 11.5% | 5.5% |
Table 2. Experimental results for the ensemble of k-NN classifiers. Classifiers based solely on a single dissimilarity and bagging have been taken as reference. (Parameters: k = 2)
In this paper, we have proposed an ensemble of classifiers based on a diversity of dissimilarities. Our approach aims to reduce the false positive error rate of classifiers based solely on a single distance. The algorithm is able to work directly from a dissimilarity matrix. The algorithm has been applied to the identification of spam messages.
The experimental results suggest that the method proposed would help to improve both misclassification errors and false positive errors. We also report that our algorithm outperforms classifiers based on a single dissimilarity and other combination strategies such as bagging.
[1] Aggarwal, C. C. Redesigning distance functions and distance-based applications for high dimensional applications. Proceedings of ACM International Conference on Management of Data and Symposium on Principles of Database Systems, vol. 1, 2001.
[2] Androutsopoulos, I.; Koutsias, J.; Chandrinosand, K. V.; Spyropoulos, C. D. An experimental comparison of naive Bayesian and keyword-based anti-spam filtering with personal email messages. 23rd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, 2000.
[3] Bauer, E.; Kohavi, R. An empirical comparison of voting classification algorithms: Bagging, boosting, and variants. Machine Learning, vol. 36, 1999.
[4] Blanco, A.; Ricket, A. M.; Martín-Merino, M. Combining SVM classifiers for e-mail anti-spam filtering. Lecture Notes in Computer Science LNCS-4507, Springer Verlag, 2007.
[6] Carreras, X.; Márquez, I. Boosting trees for anti-spam email filtering. RANLP-01, Fourth International Conference on Recent Advances in Natural Language Processing, Tzigov Chark, BG, 2001.
[8] Domingos, P. MetaCost: A general method for making classifiers cost-sensitive. ACM CM Special Interest Group on Knowledge Discovery and Data Mining, 1999.
[9] Drucker, H.; Wu, D.; Vapnik, V. N. Support vector machines for spam categorization. IEEE Transactions on Neural Networks, 10(5), 1048–1054, 1999.
[10] Fawcett, T. ‘In vivo’ spam filtering: a challenge problem for KDD. ACM Special Interest Group on Knowledge Discovery and Data Mining, 5(2), 2003.
[12] Hershkop, S.; Salvatore, J. S. Combining email models for false positive reduction. ACM Special Interest Group on Knowledge Discovery and Data Mining, 2005.
[13] Hinneburg, C. C. A. A.; Keim, D. A. What is the nearest neighbor in high dimensional spaces? Proceedings of the International Conference on Database Theory. Morgan Kaufmann, 2000.
[14] Kittler, J.; Hatef, M.; Duin, R.; Matas, J. On combining classifiers. IEEE Transactions on Neural Networks, vol. 20, no. 3, 1998.
[15] Kolcz. A.; Alspector, J. SVM-based filtering of e-mail spam with content-specific misclassification costs. Workshop on Text Mining, 1–14, 2001.
[16] Martín-Merino, M.; Muñoz, A. A new Sammon algorithm for sparse data visualization. International Conference on Pattern Recognition, vol. 1. IEEE Press, 2004.
[17] Martín-Merino, M.; Muñoz, A. Self-organizing map and Sammon mapping for asymmetric proximities. Neurocomputing, vol. 63, 2005.
[18] Pekalska, E.; Paclick, P.; Duin, R. A generalized kernel approach to dissimilarity-based classification. Journal of Machine Learning Research, vol. 2, 2001.
[19] Provost, F.; Fawcett. T. Robust classification for imprecise environments. Machine Learning, 42, 2001.
[20] UCI Machine Learning Database. Available from: http://www.ics.uci.edu/ mlearn/MLRepository.html.